TNT2 1. hefti. Talnakerfin, reikniaðgerðir og kóðar

Rökrásir og öll lógík í rafmagnsfræði byggja á tveimur stöðum. Það eru stöðurnar lokuð straumrás og opin straumrás eða spenna og ekki spenna. Til þess að lýsa þessu er notað talnakerfi sem hefur aðeins tvær stöður 0 og 1 þar sem 0 táknar annaðhvort opna straumrás eða enga spennu og 1 táknar lokaða straumrás eða spennu. Þetta talnakerfi kallast tvíundarkerfi eða binary numbers á ensku.

Áður en við hættum okkur í tvíundarkerfið og önnur kerfi þá skulum við skoða fyrst talnakerfi almennt og uppbyggingu þeirra. Þá liggur beinast við að skoða fyrst það kerfi sem við þekkjum best, tugakerfið.

Eins og við vitum þá byggist tugakerfið upp á einingum, tugum, hundruðum, þúsundum o.s.frv. Skoðum einhverja venjulega tugakerfistölu og spáum í uppbyggingu hennar. Tökum sem dæmi töluna 325. Við vitum að þetta eru 3 hundruð, 2 tugir og 5 einingar. Ef við köllum staðsetningu táknanna, í tölunni, sæti, þá er talan 5 í sætinu lengst til hægri sem ég kalla eftirleiðis 0. sæti, 2 er þá í 1. sæti og 3 í 2. sæti. Við sjáum að tugirnir sem eru í 1. sæti eru 10 sinnum stærri en einingarnar og hundruðin í 2. sæti eru 10 sinnum stærri en tugirnir. Munurinn á milli sæta er því alltaf tífaldur 1,10,100,1000…og þess vegna heitir þetta tugakerfi.

Nú skulum við skilgreina svokallaða margföldunarstuðla. Við segjum að 0. sætið hafi margföldunarstuðulinn 1 (eining), 1. sætið hefur margföldunarstuðulinn 10 (tugur), 2. sætið hefur margföldunarstuðulinn 100 (hundruð) og þannig koll af kolli. Ef við gerumst nú stærðfræðileg þá hefur 0. sætið stuðulinn 10 0 , 1. sætið stuðulinn 10 1 og 2. sætið stuðulinn 10 2 . Núna er kerfið komið þ.e. hvert sæti hefur margföldunarstuðulinn 10 númer sætis . Athugið að tala í 0. veldi er alltaf 1 sama hver talan er, nema 0.

Svona eru öll talnakerfi byggð upp. Þau hafa öll ákveðna grunntölu sem þau eru nefnd eftir. Tugakerfið hefur grunntöluna 10. Þau hafa öll ákveðinn fjölda tákna sem er sá sami og grunntalan. Tugakerfið hefur t.d. 10 tákn, tölurnar 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Í hvert sæti má aðeins koma eitt tákn og í tugakerfinu er það einhver af tölunum 0 til 9. Táknið í sætinu margfaldast síðan með margföldunarstuðli sætisins.

Þetta hljómar flókið er svona eru öll talnakerfi byggð upp. Við erum orðin svo vön því að nota tugakerfið að við leiðum aldrei hugann að uppbyggingu þess. Ef við hinsvegar áttum okkur á henni þá er lítið mál að læra ný talnakerfi.

Grunntala = 10

Fjöldi tákna = 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

Dæmi: Talan 793 er 7 · 10 2 + 9 · 10 1 + 3 · 10 0 = 7 · 100 + 9 · 10 + 3 · 1 = 700 + 90 + 3 = 793 10 (fótskrift 1100 er til þess að tilgreina í hvaða kerfi við erum að vinna ).

Tugakerfið hefur líka brothluta þ.e. tölur aftan við kommu. Þær fylgja líka ákveðnu kerfi. Við tölum um 1/10, 1/100, 1/1000 o.s.frv. Sjáum að nefnarinn stækkar tífalt eftir því sem við förum lengra til hægri. Það er vegna þess að við erum í talnakerfi með grunntöluna 10. Tölur vinstra megin við kommu stækka tífalt við hvert sæti en tölur hægra megin við kommu minnka tífalt við hvert sæti. Uppbyggingin lítur svona út.

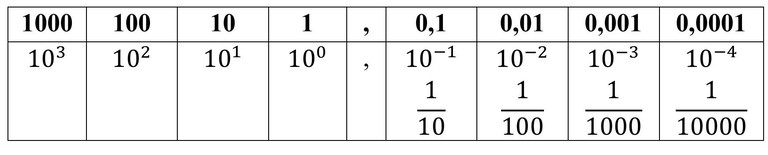
Talan 17,53 er því 110 + 7 · 1 (+) 5 · 0,1 + 3 · 0,01 (+) = viðbót aftan við kommu.